こんにちは、最近の暑さで夏バテ気味なSayahamittです。 大学の学期末テストとそれに伴う課題ラッシュが終わりました。 その課題の一つに「食事をする哲学者問題」を解くアルゴリズムをC言語で実装しろ、 というものが有ったので、僕なりに解こうとした過程と結果を綴りたいと思います。
以下、無知な初心者のほざき、覚書
説明が下手くそなので、完動コードに目を通して頂けると多少は読みやすくなる…と思います(´・ω・`)
食事をする哲学者問題ってなんぞやという話ですが、端的には共有資源の取り合いの問題です。
具体的には…
中央に大皿料理が置かれた円卓に5人の哲学者が座っていて、それぞれの哲学者の間に一本ずつフォークが置いてあります。哲学者は食事をする際には2本のフォークを使う必要があるものとして、現実的な時間以内に食事が出来ないと餓死してしまいます。さらに、それぞれの哲学者が一度の食事に掛かる時間はまちまちで、予測不可能な状態です。
この状況下で、全ての哲学者が同一のルールに基いて行動している限り全員が餓死すること無くコンスタントに食事が出来るようなアルゴリズムを考案せよ。 というのが「食事をする哲学者問題」です。
Wikipedia : 食事をする哲学者問題
プログラムを考える上で、まず幾つかの仮定/制限を行います。
各哲学者はフォークを取るとき、片手ずつ取ろうとする。
各哲学者の行動(フォーク取得アルゴリズム)はそれぞれ別々のスレッドで実行される。
共有資源であるフォークにアクセスする作業はセマフォで管理する。
哲学者の挙動を定義する関数は一つしか作らない。
セマフォの操作にはsem_init , sem_destroy , sem_wait , sem_post以外の関数を用いない。(講義で取り扱っていないため。)
セマフォのPasseren,Verhoogによってのみフォークを取ったり置いたりできる。
それから出来ればこうしたい、という希望…
N人の哲学者がいる場合に対応させたい。
初期状態から全ての哲学者の処理が完全に同期して行われた場合にも対応させたい。
さて、Wikipediaの記事にも色々な解が載っていますが情弱だった僕はググることもせずに思案に熱中していたため、妙にダサいオリジナリティあふれるアルゴリズムが出来てしまいました。問題に対する理解も浅く、他の解もあまり調べないでテキトーに考えた解なので、本当に題意に沿う正しいものなのか自信はありませんが幼稚な心が見せびらかしたいと騒ぐので記事にしている次第です。
アルゴリズムを考える上でまず始めに思いつく最悪の状態は、「全員が同時に同じ側のフォークを取ること」です。仮にフォークを取る時に利用するセマフォの初期値がフォークの本数と同じ5本だった場合、5人が同時にsem_waitを行うとめでたくデッドロックの完成です。しかしそれでは困るわけで、上記の仮定/制限下で食事をする哲学者問題を解くには「全員が同時に同じ側のフォークを取ろうとしてもデッドロックを回避でき、かつ全員が食事を出来る事を保証するアルゴリズム」を考える必要があります。
また、安易なsem_waitはスレッドをセマフォ待ちに釘付けにしてしまうので行うべきはありません。そのためにはまずsem_wait関数を叩く以外の方法で各哲学者がフォークの状態(置かれているか使われているか)を知る仕組みを作る必要があります。普通ならsem_getvalueを使えばいいのですが、今回はそれが使えないという縛り(授業でやっていないからと言って使わせてくれない)があるので別の方法を考えねばなりません。
それでどうしたかと言うと、定石通り構造体を使いました。
哲学者一人を表す構造体をこのように定義します。
typedef struct Philosopher{
int id; //哲学者を識別する番号
int forkleft; //左手でフォークを取ろうとする時にtrue
int forkright; //右手でフォークを取ろうとする時にtrue
pthread_t phil_thread; //自身の処理を行うスレッド
struct Philosopher *prev; //右側の哲学者を指すポインタ
struct Philosopher *next; //左側の哲学者を指すポインタ
}Philosopher;
そして、これをリング構造で繋いでやろうという魂胆です。
リストではなくリングにすることで、左右へのポインタについて末端で特別な処理をする必要がなくなります。
そして、pthreadで作る哲学者の処理を行うスレッドに自身の構造体へのポインタを渡してやるようにするのです。そうすればスレッド内部からmain内で生成された自分の構造体が参照出来ます。
Philosopher header; //リングの基点を指し示す為のダミー
void *Phil(Philosopher* me); //哲学者の行動を記述した関数の宣言
int main(void){
Philosopher *pointer;
/*何かの処理*/
for(i=0,pointer=header.next; i<N; i++){
res1 = pthread_create(&(pointer->phil_thread),NULL,Phil,pointer);
pointer=pointer->next;
}
/*何かの処理*/
}
肝心なセマフォですが、今回はグローバルスコープでForks_semを宣言し初期値を哲学者の人数より一つ少ない値にします。また、フォークを戻す時にwaitするSpaces_semも同様に定義します。
#define N 5 //哲学者の人数
sem_t Forks_sem;
sem_t Spaces_sem;
int main(void){
/*何かの処理*/
res0 = sem_init(&Forks_sem,0,N-1);
res0 = sem_init(&Spaces_sem,0,0);
/*何かの処理*/
}
これで枠組みは出来ました。あとは核心となるアルゴリズムです。
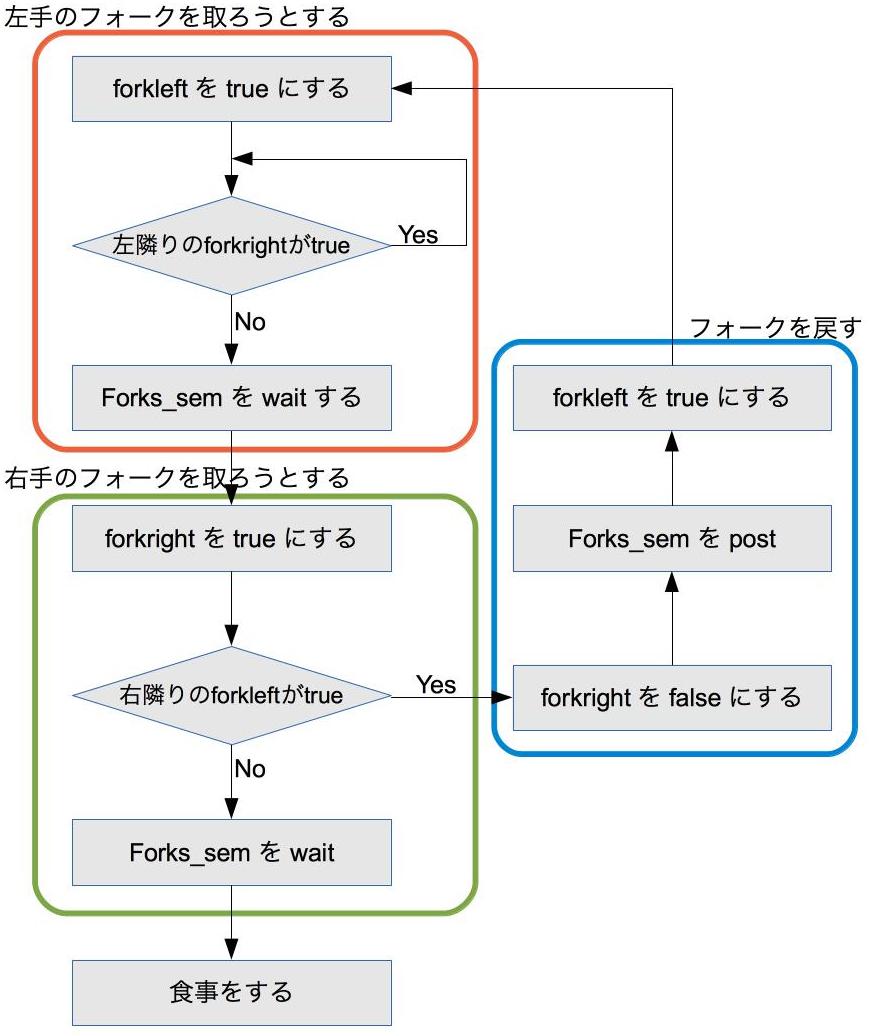
これを実装した関数がこちら
void *Phil(Philosopher* me){
int diningtime;
while(1){
while(1){
//forkleftをtrue にする
me->forkleft=1;
//左隣りのforkrightがtrue?
while(me->next->forkleft==1){}
//Forks_semをwaitする
sem_wait(&Forks_sem);
sem_post(&Spaces_sem);
//forkrightをtrueにする
me->forkright=1;
//右隣りのforkleftがtrue?
if(me->prev->forkleft!=1){
//Forks_semをwait
sem_wait(&Forks_sem);
sem_post(&Spaces_sem);
break;//食事へ
}
//forkrightをfalseにする
me->forkleft=0;
//Forks_semをpost
sem_post(&Forks_sem);
sem_wait(&Spaces_sem);
//forkleftをtrueにする
me->forkright=0;
sleep(1);
}
//食事をする
printf("哲学者%d:食事をする\n",me->id);
diningtime=Diningtime();
printf(">>>哲学者%d:食事中(時間=%d秒)\n",me->id,diningtime);
sleep(diningtime);
printf("---哲学者%d:完食\n",me->id);
//左手のフォークを戻す
sem_wait(&Spaces_sem);
sem_post(&Forks_sem);
me->forkleft=0;
//右手のフォークを戻す
sem_wait(&Spaces_sem);
sem_post(&Forks_sem);
me->forkright=0;
sleep(1);
}
}
int Diningtime(){
return 1+(int)(9.0*rand()/RAND_MAX+1.0);
}
このアルゴリズムは何をやっているかというと、
ある哲学者がフォークを取ろうとする時には、まず何はともあれforkleft/right変数をtrueにして自分がフォークを取ろうとしている時に他人に邪魔されないようにしているわけです。
また、あるフォークを取ろうとした時に、そのフォークが既に他の哲学者によって取ろうとされていた場合はその哲学者がフォークを置くまで待つ。その時に一本フォークを持っていればそれは置き最初からやり直す、ということになっています。
セマフォの初期値を人数より一つ少ない値にすることと、上記のルールを適用することで、5人が同時に左側のフォークを取ろうとしても、一人必ずセマフォ待ちが発生してそこで待たされ、その間に他の哲学者達がフォークを戻して(セマフォをpost)くれるので、待っていた一人が必ず食べられるということになります。
これでデッドロックを防ぎつつ、誰も特別扱いせずに食事をする哲学者問題を解く事が出来ました。ただ、一つだけ問題があります、このアルゴリズムではセマフォの初期値を人数より一つ少ない値にする必要があるので哲学者が2人の時は使えません。また、4人の時は最初に食事を始めた一人とその向いに座っている哲学者しか食べられません。
このアルゴリズムで上記2つの課題を完全に解決するのは難しそうです。(´・ω・`) 完全で無い解決方法はありますが、それは書いても仕方がないでしょう。
でもまぁ…食事をする哲学者問題は大抵5人以上で論じられている事が多いし…
まぁいいか( ´∀`)つ ミ
細かい動作は完動コードが無いと分からないので載せておきます。
ではでは ノシ